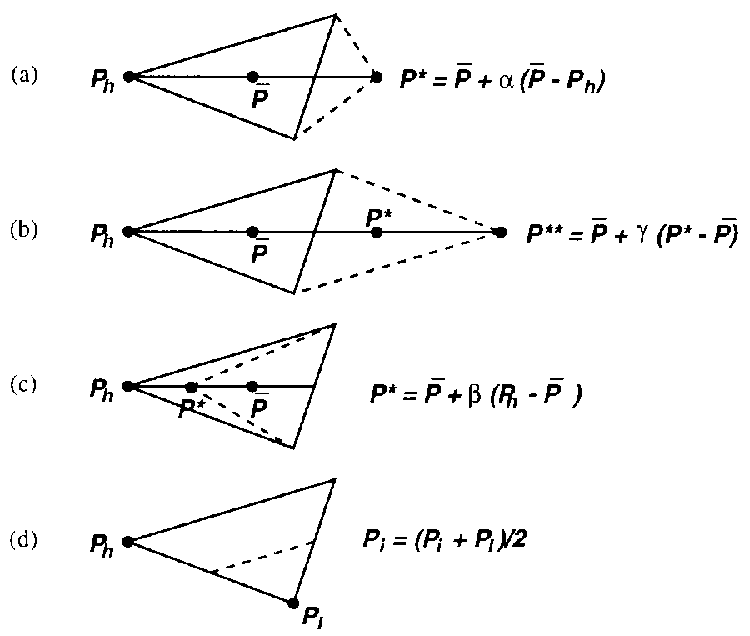CS4601: Introduction to Intelligent Computing
Downhill Simplex Search
 Basic Concept:
Basic Concept:
A simplex is a collection of n+1
points in n-dimensional space.
The downhill simplex search repeatedly
replaces the point having the highest function value in a simplex
with another point.
When combined with other operations, the simplex
under consideration adapts itself to the local landscape,
elongating down long inclined planes, changing direction on
encountering a valley at an angle,
and contracting in the neighborhood of a minimum.
 Initialization:
Initialization:
To start the downhill simplex search, we must initialize a simplex of
n+1 points. For example, a simplex is a triangle in
two-dimensional space and a tetrahedron in three-dimensional space.
Moreover, we would like the simplex to be nondegenerate--that is, it
encloses a finite inner n-dimensional volume.
An easy way to set up
a simplex is to start with an initial starting point
 and the
other n points can be taken as
and the
other n points can be taken as

where
 's
are unit vectors consisting of a basis of the
n-dimensional space and
's
are unit vectors consisting of a basis of the
n-dimensional space and
 is a constant reflecting the guess of the characteristic
length scale of the optimization problem in question.
is a constant reflecting the guess of the characteristic
length scale of the optimization problem in question.
We write
 for the function value at
for the function value at
 and let
and let

In other words, l and h are respectively the indices
for the minimum and maximum of
 .
In symbols,
.
In symbols,

Let
 be the average (centroid) of these n+1 points.
Each cycle of this method starts with a reflection point
be the average (centroid) of these n+1 points.
Each cycle of this method starts with a reflection point
 of
of  .
Depending on the function value at
.
Depending on the function value at
 ,
we have four possible operations to change the current simplex
to explore the landscape of the function efficiently in
multidimensional space.
These four operations are
(1) reflection away from
,
we have four possible operations to change the current simplex
to explore the landscape of the function efficiently in
multidimensional space.
These four operations are
(1) reflection away from
 ;
(2) reflection and expansion away from
;
(2) reflection and expansion away from
 ;
(3) contraction along one dimension connecting
;
(3) contraction along one dimension connecting
 and
and
 ; and
(4) shrinkage toward
; and
(4) shrinkage toward
 along all dimensions.
When f is a two-input function,
these four operations are shown in the following figure.
along all dimensions.
When f is a two-input function,
these four operations are shown in the following figure.
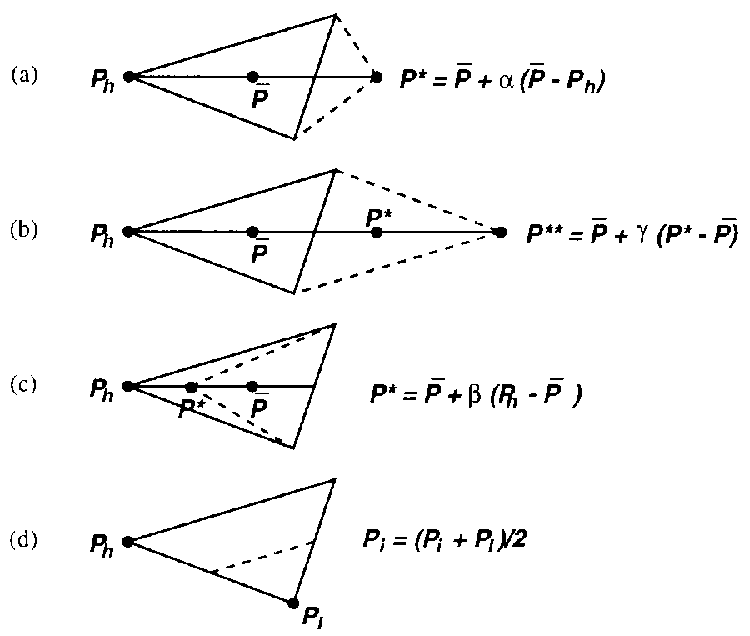
|
- (a) reflection away from
 ; ;
- (b) reflection and expansion away from
 ; ;
- (c) contraction along one dimension connecting
 and and
 ; ;
- (d) shrinkage toward
 alone all dimensions.
alone all dimensions.
|
Before describing the full cycle of the simplex search, we need to
define four intervals to be used in the search process:
- Interval 1:

- Interval 2:

- Interval 3:

- Interval 4:
 .
.
These intervals are shown next.
|
|
Four intervals used in the downhill simplex search.
|
 A Full Cycle of Downhill Simplex Search:
A Full Cycle of Downhill Simplex Search:
A full cycle of the downhill simplex search involves the following
four steps:
- Reflection:
- Define the reflection point
 and its value
and its value
 as
as

where the reflection coefficient
 is a positive constant. Thus
is a positive constant. Thus
 is on the line joining
is on the line joining
 and
and  ,
on the far side of
,
on the far side of
 from
from
 .
Depending on the value of
.
Depending on the value of
 ,
we have the following actions:
,
we have the following actions:
- If
 is in interval 1, go to
expansion.
is in interval 1, go to
expansion.
- If
 is in interval 2, replace
is in interval 2, replace
 with
with
 and finish this cycle.
and finish this cycle.
- If
 is in interval 3, replace
is in interval 3, replace
 with
with
 and go to contraction.
and go to contraction.
- If
 is in interval 4, go to contraction.
is in interval 4, go to contraction.
- Expansion:
- Define the expansion point
 and its value
and its value
 as
as

where the expansion coefficient
 is greater than unity.
If
is greater than unity.
If  is in interval 1, replace
is in interval 1, replace
 with
with
 and finish this cycle. Otherwise, replace
and finish this cycle. Otherwise, replace
 with the original reflection point
with the original reflection point
 and finish this cycle.
and finish this cycle.
- Contraction:
- Define the contraction point
 and its value
and its value
 as
as

where the contraction coefficient
 lies between 0 and 1.
If
lies between 0 and 1.
If  is in interval 1, 2, or 3, replace
is in interval 1, 2, or 3, replace
 with
with
 and finish this cycle. Otherwise, go to shrinkage.
and finish this cycle. Otherwise, go to shrinkage.
- Shrinkage:
- Replace each
 with
with
 .
Finish this cycle.
.
Finish this cycle.
The foregoing cycle is repeated until a given stopping criterion is met.
A complete flow chart of the foregoing steps is given next.

|
|
Flowchart for downhill simplex search.
|
Before starting using this method, we still need to determine three
constants
 ,
,
 and
and
 ,
which are the coefficients for reflection, contraction, and expansion.
Generally speaking, the optimal values for these coefficients are
application dependent, and the best way to select their values is
by doing some trial-and-error experiments.
A good starting point is
,
which are the coefficients for reflection, contraction, and expansion.
Generally speaking, the optimal values for these coefficients are
application dependent, and the best way to select their values is
by doing some trial-and-error experiments.
A good starting point is
 ;
these values are suggested in Nelder and Mead's original paper.
;
these values are suggested in Nelder and Mead's original paper.
 Downhill Simplex Search for Continuous Optimization:
An Example:
Downhill Simplex Search for Continuous Optimization:
An Example:
Find the min. of the peaks function:
z = peaks(x, y)
= 3*(1-x)^2*exp(-(x^2) - (y+1)^2)
- 10*(x/5 - x^3 - y^5)*exp(-x^2-y^2) - 1/3*exp(-(x+1)^2 - y^2).

|
|
|
Surface plot of z = peaks(x, y)
|
Contour plot of z = peaks(x, y)
|
Simplex search process:
(You can watch the animation of simplex search for the "peaks"
function by executing the MATLAB file
go_simp.m located at
ftp://ftp.cs.nthu.edu.tw/pub/CS/papers/jang/book/soft. Other
auxiliary files are:
peaksfcn.m.)
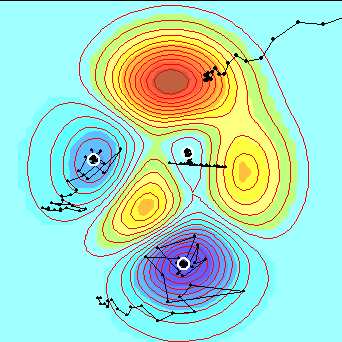
|
|
An example of simplex search
|
 Advantages of Simplex Search:
Advantages of Simplex Search:
- Derivative-free
(derivatives of the peaks function).
- Interesting geometric interpretation
 Weakness of Simplex Search:
Weakness of Simplex Search:
- Slow
- Not stochastic
- Underlying heuristics are only good for continuous optimization.
 Reported Simplex Search Applications:
Reported Simplex Search Applications:
- Neural networks modeling
- Fuzzy modeling
- All kinds of continuous optimization
 Reference:
Neuro-Fuzzy and Soft Computing
Reference:
Neuro-Fuzzy and Soft Computing
This page is maintained by
Jyh-Shing Roger Jang.
Comments and suggestions are welcome:
jang@cs.nthu.edu.tw.
 Basic Concept:
Basic Concept: