Problem D

Bang the Drum Slowly

Input File: drum.in

Many years ago the "primary memory" of most computer systems was a magnetic drum. Read/write heads were placed so they could access data from the magnetic outer surface as the drum rotated along its horizontal axis. The following illustration gives the basic idea:

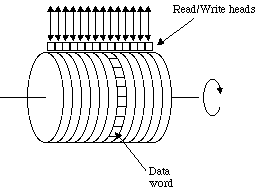
As the drum rotated, the data word under the read/write head(s) could be accessed. The drum continued to rotate after an instruction was fetched. After the execution of an instruction, the word ready to be accessed by the read/write head(s) was typically many words away. To minimize the delay that would occur if instructions to be executed sequentially were placed in consecutive words on the drum, designers of these machines frequently included the next instruction's drum address as a field in the instruction (that is, each instruction included an explicit "next instruction" address). Then "optimizing" assemblers could fill in the next instruction field with the address of the first available word ready to be read by the drum as soon as the current instruction was completed.

In this problem we want to determine the average execution times of simple programs without loops. We will consider only a single read/write head on a single track. Assume that the words on that track have sequential addresses numbered 1 through n. All instructions require the same length of time to execute, specifically the same time as it takes the drum to rotate past t words. t does not include the time to read the instruction from the drum, nor does it include the additional rotational delay that might be required if the next instruction isn't at the "optimum" address. However, these factors must be included in calculating the average execution time.

There are three types of instructions: terminal, conditional and unconditional. Terminal instructions don't have a "next instruction" address, since they terminate the execution of a program. Conditional instructions have two "next instruction" addresses, and unconditional instructions have only one "next instruction" address.

The execution time of a program run is the time taken from beginning to read the first instruction until the terminal instruction has executed. To calculate the average execution time of a program, every possible run time is weighted (multiplied) by the probability of the run. We assume equal probability of taking each path of a branch in a conditional instruction. The sum of all weighted run times is the average execution time of the program.

Assumptions

Input

The input consists of a number of test cases. The input for each test case begins with a line containing integer values for n (1 < n < 50) and t (0 < t < n). This line is followed by a sequence of lines each of which contains integers representing an instruction address and zero, one, or two branch addresses. Specifically, for each instruction there is a location (between 1 and n), the number of "next instruction" addresses (0 for a terminal instruction, 1 for an unconditional instruction, and 2 for a conditional instruction), and that many branch addresses. The last instruction is followed by 0 on a line by itself. The input set is terminated by values of 0 for both n and t.

Output

For each test case, print the case number (they are numbered sequentially starting with 1) and the average execution time for the program. Execution times must be accurate to and displayed with four fractional digits.

Sample Input 

10 5
1 0
0
10 5
1 1 6
6 0
0
10 5
1 1 7
7 0
0
10 5
1 2 7 8
7 0
8 0
0
10 6
8 0
7 1 3
3 0
1 2 7 8
0
0 0

Output for the Sample Input 

Case 1. Execution time = 6.0000
Case 2. Execution time = 21.0000
Case 3. Execution time = 12.0000
Case 4. Execution time = 12.5000
Case 5. Execution time = 26.5000