Problem Set

Contents

1. Stars
2. Hexagon
3. Domino Effect
4. Pendulum
5. Border
6. The New Villa
7. Ships
8. Jury Compromise

Problem A: Stars

Given a sketch of the constellation, it is not easy for the amateur to actually find the constellation in the sky. Moreover, simple constellations, such as ``Triangulum'' (triangle,) which consists of only three stars, may appear several times in the sky. Again, singling out the ``correct'' occurrence is not easy.

Traditionally, maps were printed for just this purpose. But in this problem, we will see how the computer can help us find constellations in the sky.

You will be given a star map; for simplicity this will be a collection of points in the plane, each having a certain brightness associated with it. Then, given a constellation, also as a set of points in the plane, you are to determine:

• the number of occurrences of the constellation in the star map, and
• the position of the brightest occurrence, if one exists. (The rationale behind this is as follows: if a constellation seems to appear several times in the sky, the brightest one is most likely to be the real one, since it is the most eye-catching one.)

The brightness of an occurrence is the average brightness of the stars it consists of, i.e. the sum of individual brightnesses divided by the number of stars in the constellation.

Input Specification

The next line contains a single integer m, the number of constellations to follow (1 <= m < 50). Each constellation description starts with a line containing an integer s_i, the number of stars in constellation i, and a string N_i, the name of the constellation. (N_i will consist of no more than 40 characters and contain no blanks.) The following s_i lines then contain the coordinates of the constellation, again as x/y-pairs.

A blank line separates the star map from the next map. The input file ends with an empty map (having n = 0), which should not be processed.

N.B.: Since all star coordinates are integer numbers, you can easily rule out any rotated or scaled constellation whose points do not fall on integer coordinates.

Output Specification

For each constellation, in the same order as in the input, output first its name and how many times it occurs in the map on one line, as shown in the output sample.

If there is at least one occurrence, output the position of the brightest occurrence by listing the positions of the stars that form the brightest occurrence. The star positions have to be printed in ascending x-order. Positions having the same x-coordinates must be sorted in ascending y-order. If there are several equally bright solutions, output only one of them. Adhere to the format shown in the sample output.

Output a blank line before each constellation and a line of 5 dashes (`-----') after every star map.

Sample Input

6
1 2 1
2 1 4
2 4 3
3 2 1
4 1 5
4 3 2
2
3 Triangulum
1 1
3 1
2 4
4 Cancer
1 3
4 3
6 1
7 5

0

Output for Sample Input

Map #1

Triangulum occurs 2 time(s) in the map.
Brightest occurrence: (1,2) (4,1) (4,3)


Cancer occurs 0 time(s) in the map.

-----

Problem B: Hexagon

The game board has to be completely covered using a set of hexagonal pieces. Each piece carries three numbers, one for every primary board direction. Only three different numbers are used for each direction. Every possible combination of three numbers for all three directions is assigned to a piece, leading to a set of 27 unique pieces. (The board in the above figure is still in the process of being covered.)

The score of a board is calculated as the sum of all 15 row scores (5 rows for each primary direction). The row scores are calculated as follows: if all pieces in a row carry the same number for the direction of the row, the row score is this number multiplied by the number of pieces in the row. Otherwise (the pieces carry different numbers in the row direction) the row score is zero. Note that the pieces may not be rotated. For example, the score of the leftmost row in the figure is 3 ^. 3 = 9, the score of the row to its right is 4 ^. 11 = 44.

While in the real game the pieces are chosen randomly and the set of pieces is fixed, we are interested in the highest possible score for a given set of numbers for each direction. This means you have to choose those 19 pieces that result in the highest score.

Input Specification

Output Specification

Sample Input

1
9 4 3
8 5 2
7 6 1

Output for Sample Input

Test #1
308

The following clarification was added to the problem during the last minute announcements:
To simplify the problem, you should only consider boards where each row has a score greater than zero, i.e. each piece in a row carries the same number.

Problem C: Domino Effect

While this is somewhat pointless with only a few dominoes, some people went to the opposite extreme in the early Eighties. Using millions of dominoes of different colors and materials to fill whole halls with elaborate patterns of falling dominoes, they created (short-lived) pieces of art. In these constructions, usually not only one but several rows of dominoes were falling at the same time. As you can imagine, timing is an essential factor here.

It is now your task to write a program that, given such a system of rows formed by dominoes, computes when and where the last domino falls. The system consists of several ``key dominoes'' connected by rows of simple dominoes. When a key domino falls, all rows connected to the domino will also start falling (except for the ones that have already fallen). When the falling rows reach other key dominoes that have not fallen yet, these other key dominoes will fall as well and set off the rows connected to them. Domino rows may start collapsing at either end. It is even possible that a row is collapsing on both ends, in which case the last domino falling in that row is somewhere between its key dominoes. You can assume that rows fall at a uniform rate.

Input Specification

The following m lines each contain three integers a, b, and l, stating that there is a row between key dominoes a and b that takes l seconds to fall down from end to end.

Each system is started by tipping over key domino number 1.

The file ends with an empty system (with n = m = 0), which should not be processed.

Output Specification

Sample Input

2 1
1 2 27
3 3
1 2 5
1 3 5
2 3 5
0 0

Output for Sample Input

System #1
The last domino falls after 27.0 seconds, at key domino 2.


System #2
The last domino falls after 7.5 seconds, between key dominoes 2 and 3.

Problem D: Pendulum

More formally, we place a cartesian coordinate system on the wall. The pendulum's string is affixed at the origin (0, 0). As usual, the x-axis points to the right and the y-axis points upwards. The string of the pendulum has a length of r. The pendulum is released at position (-r, 0) and therefore starts swinging to the right. Furthermore, there are n additional hooks distributed over the plane which may influence the path of the pendulum.

In our ideal world, the following assumptions are true:

• The diameters of the hooks and of the string are zero.
• The pendulum loses no energy (e.g. by friction).
• The pendulum will never hit a hook, only its string will.
• The pendulum's string is made of some futuristic material that only bends where it touches a hook but is otherwise rigid.

Input Specification

The file ends with a case having r = 0, which should not be processed.

Output Specification

Then print a line that contains the distance which the pendulum travels for completing one cycle of its periodic orbit. Do not count the distance travelled to reach the starting point of the orbit. (Adhere to the format shown in the output sample.) The distance should be exact to two digits to the right of the decimal point.

Output a blank line after each test case.

Sample Input

2 16.0
3 -4
-3 -4
1 18.0
5 -12
0 0

Output for Sample Input

Pendulum #1
Length of periodic orbit = 87.66


Pendulum #2
Length of periodic orbit = 31.42

Problem E: Border

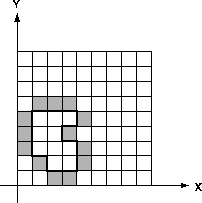
The path is closed and runs along the grid lines, i.e. between the squares of the grid. The path runs counter-clockwise, so if following the path is considered as going ``forward'', the border pixels are always to the ``right'' of the path. The bitmap always covers 32 by 32 squares and has its lower left corner at (0, 0). You can safely assume that the path never touches the bounding rectangle of the bitmap and never touches or crosses itself. Note that a bit gets set if it is on the outside of the area surrounded by the path and if at least one of its edges belongs to the path, but not if only one of its corners is in the path. (A look at the convex corners in the figure should clarify that statement.)

Input Specification

Output Specification

Sample Input

1
2 1
EENNWNENWWWSSSES.

Output for Sample Input

[End of Problem E]

Problem F: The New Villa

One night, Mr. Black came home late. While standing in the hallway, he noted that the lights in all other rooms were switched off. Unfortunately, Mr. Black was afraid of the dark, so he never dared to enter a room that had its lights out and would never switch off the lights of the room he was in.

After some thought, Mr. Black was able to use the incorrectly wired light switches to his advantage. He managed to get to his bedroom and to switch off all lights except for the one in the bedroom.

You are to write a program that, given a description of a villa, determines how to get from the hallway to the bedroom if only the hallway light is initially switched on. You may never enter a dark room, and after the last move, all lights except for the one in the bedroom must be switched off. If there are several paths to the bedroom, you have to find the one which uses the smallest number of steps, where ``move from one room to another'', ``switch on a light'' and ``switch off a light'' each count as one step.

Input Specification

This line is followed by d lines containing two integers i and j each, specifying that room i is connected to room j by a door. Then follow s lines containing two integers k and l each, indicating that there is a light switch in room k that controls the light in room l.

A blank line separates the villa description from the next one. The input file ends with a villa having r = d = s = 0, which should not be processed.

Output Specification

If there is a solution to Mr. Black's problem, output the shortest possible sequence of steps that leads him to his bedroom and only leaves the bedroom light switched on. (Output only one shortest sequence if you find more than one.) Adhere to the output format shown in the sample below.

If there is no solution, output a line containing the statement `The problem cannot be solved.'

Output a blank line after each test case.

Input Sample

3 3 4
1 2
1 3
3 2
1 2
1 3
2 1
3 2

2 1 2
2 1
1 1
1 2

0 0 0

Output for Input Sample

Villa #1

The problem can be solved in 6 steps:
 - Switch on light in room 2.
 - Switch on light in room 3.
 - Move to room 2.
 - Switch off light in room 1.
 - Move to room 3.
 - Switch off light in room 2.


Villa #2
The problem cannot be solved.

Problem G: Ships

In our version of the game, your opponent has distributed the following seven ship patterns over a rectangular grid of squares:

xx  xx    xx  x      x   x
xx   xx  xx   xxx  xxx  xxx  xxxx

Each ship pattern covers exactly four squares. The patterns may be rotated but not mirrored. All patterns are guaranteed to be placed completely within the boundaries of the rectangle and not to overlap each other, whereas touching another pattern or the border is allowed.

We assume that we are in the middle of the game and that several squares have already been uncovered. You will be given a rectangular grid of squares representing your current knowledge about the positions of your enemy's ships. Every square is marked by one of the following characters:

• `x' if a ship covers the square
• `o' if no ship covers the square
• `.' if the square has not yet been uncovered

Input Specification

Each of the next h lines contains a string of w characters. Each of these characters is either `x', `o' or `.', depending on the state of the corresponding square.

A blank line separates each game from the next. The input file ends with a game having w = 0 and h = 0. This game should not be processed.

Output Specification

Output a blank line after every game.

Sample Input

10 10
.x..x.....
oooooxoooo
oxooxxx...
xxoooooo..
xoooxooo..
ooxxxxoo..
oooooxxoox
ooooooxoox
ooooooooxx
oooooooooo


0 0

Output for Sample Input

Game #1
yes.

Problem H: Jury Compromise

Based on the grades of the two parties, the judge selects the jury. In order to ensure a fair trial, the tendencies of the jury to favour either defence or prosecution should be as balanced as possible. The jury therefore has to be chosen in a way that is satisfactory to both parties.

We will now make this more precise: given a pool of n potential jurors and two values d_i (the defence's value) and p_i (the prosecution's value) for each potential juror i, you are to select a jury of m persons. If J is a subset of {1,...,n} with m elements, then D(J) = sum_{k in J} d_k and P(J) = sum_{k in J} p_k are the total values of this jury for defence and prosecution.

For an optimal jury J, the value |D(J) - P(J)| must be minimal. If there are several jurys with minimal |D(J) - P(J)|, one which maximizes D(J) + P(J) should be selected since the jury should be as ideal as possible for both parties.

You are to write a program that implements this jury selection process and chooses an optimal jury given a set of candidates.

Note: If your solution is based on an inefficient algorithm, it may not execute in the allotted time.

Input Specification

The file ends with a round that has n = m = 0.

Output Specification

On the next line print the values D(J) and P(J) of your jury as shown below and on another line print the numbers of the m chosen candidates in ascending order. Output a blank before each individual candidate number.

Output an empty line after each test case.

Sample Input

4 2
1 2
2 3
4 1
6 2


0 0

Output for Sample Input

Jury #1
Best jury has value 6 for prosecution and value 4 for defence:
 2 3

 Last update: November 28, 1996 (eos).