The figure drawn by these commands is illustrated to the right. Each
of the lines is exactly one inch long. PostScript ® is widely used as a page description language for laser printers. The basic unit of measurement in PostScript is the point, and there are assumed to be exactly 72 points per inch. The default coordinate system used at the beginning of a PostScript program is the familiar Cartesian system, with the origin (the point with x and y coordinates both equal to zero) at the lower left corner of the page.
In this problem you are required to recognize a small part of the PostScript language. Specifically, the commands listed below must be recognized. All commands will be given in lower-case letters. When the word number appears in the command description, a floating point value, with an optional sign and decimal point will be present in the input data. When two numbers appear in a command, the first refers to the x coordinate, and the second to the y coordinate. For simplicity, each command will appear on a line by itself, and a single blank will separate each component of the command. The end of line character will immediately follow each command, and a line with a single asterisk in column one will terminate the input.
number rotate number represents the measure of an angle.
This command rotates the coordinate system that may degrees counter clockwise
about the current origin. his does not affect any lines that have already
been drawn on the page. Example: 90 rotate
will rotate the axes 90 degrees counterclockwise, so the positive y axis
now points to the left, and the positive x axis points up. number number translate 612
792 translate would move the origin of the coordinate system
to the upper right corner of the page. Now only points with negative x
and y components will correspond to points on the physical page (assuming
an 8.5" by 11" page in the portrait orientation). number number scale 3 2 scale would cause
a line drawn from (0,0) to (72,72) to appear as if it was drawn from the
lower left corner of the page to a point three inches to the right of the
left edge of the paper and two inches up from the bottom edge of the paper,
assuming the original coordinate system was in effect just before the command.
number number moveto 72
144 moveto would move the current point to one inch from
the left edge of the paper, and two inches up from the bottom edge, assuming
the original coordinate system was in effect. number number rmoveto moveto, except the
numbers specified give the coordinates of the new current point relative
to the current position. Example: 144 -36 rmoveto
would move the current point set by the previous example two inches further
to the right and one-half inch lower on the page. Thus the coordinates
of the current point become (216,108). Notice that numbers can be negative!
number number lineto number number rlineto lineto, but the coordinates
given in the command are relative o the current position. Again, the end
of the line that is drawn becomes the new current position. Example: 0
144 rlineto will draw a two inch horizontal line from the
current position two inches to the right. Using the current position left
in the previous example, this draws a line from (216,144) to (216,288),
and leaves the current point at (216,288). Your task is to read one of these small PostScript programs and to display
a program that will produce the same effect without using the rotate,
translate, or scale
commands. That is, each moveto, rmoveto,
lineto, and rlineto
command in the original (input) program should appear in your output (most
likely with modified numbers), but the rotate,
translate, and scale
commands in the input must not appear in the output. Assume the original
coordinate system is in effect at the beginning of execution. The numbers
used with the commands in the program you produce must be accurate to at
least two fractional digits.
300 300 moveto 0 72 rlineto 2 1 scale 36 0 rlineto 1 -4 scale 0 18 rlineto 1 -0.25 scale 0.5 1 scale 300 300 translate 90 rotate 0 0 moveto 0 72 rlineto 2 1 scale 36 0 rlineto 1 -4 scale 0 18 rlineto *
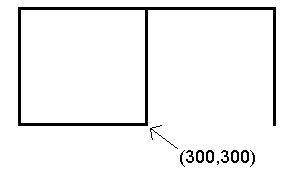
300 300 moveto 0 72 rlineto 72 0 rlineto 0 -72 rlineto 300 300 moveto -72 0 rlineto 0 72 rlineto 72 0 rlineto
400 500 moveto 300 400 lineto 0.5 0.4 scale 200 200 lineto 95 rotate 250 -200 lineto -100 -100 translate 0.5 0.1 scale 250 70 lineto 250 70 rmoveto 150 250 rlineto *
400 500 moveto 300 400 lineto 100 80 lineto 88.725 106.592 lineto 45.2336 13.2041 lineto -8.93393 49.5657 rmoveto -15.7208 29.0143 rlineto
The figure drawn by these commands is illustrated to the right. Each
of the lines is exactly one inch long.