 |
tanmlp.m
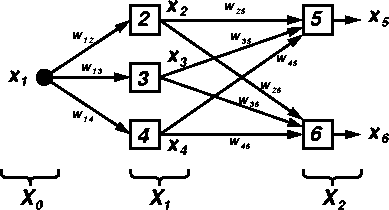
For simplicity, suppose that we are dealing with a 1-3-2 multilayer
perceptron with hyperbolic tangent activation functions, and we have
100 input-output data pairs as the training data set.
The training data set can be represented by a
![]() matrix:
matrix:
![\begin{displaymath}
\left[
\begin{array}
{ccc}
x_{1,1} & t_{5,1} & t_{6,1} \\ \v...
...dots \\ x_{1,100} & t_{5,100} & t_{6,100} \\ \end{array}\right]\end{displaymath}](img3.gif)
![\begin{displaymath}
{\bf X}_0 =
\left[
\begin{array}
{ccc}
x_{1,1} \\ \vdots \\ x_{1,p} \\ \vdots \\ x_{1,100} \\ \end{array}\right]\end{displaymath}](img5.gif)
![\begin{displaymath}
{\bf T}=
\left[
\begin{array}
{cc}
t_{5,1} & t_{6,1} \\ \vdo...
... \vdots & \vdots \\ t_{5,100} & t_{6,100} \\ \end{array}\right]\end{displaymath}](img7.gif)
For discussion convenience, we shall also defined ![]() and
and ![]() as the node outputs for layer 1 and 2, respectively:
as the node outputs for layer 1 and 2, respectively:
![\begin{displaymath}
{\bf X}_1 =
\left[
\begin{array}
{ccc}
x_{2,1} & x_{3,1} & ...
...dots \\ x_{2,100} & x_{3,100} & x_{4,100} \\ \end{array}\right]\end{displaymath}](img10.gif)
![\begin{displaymath}
{\bf X}_2 =
\left[
\begin{array}
{cc}
x_{5,1} & x_{6,1} \\ ...
... \vdots & \vdots \\ x_{5,100} & x_{6,100} \\ \end{array}\right]\end{displaymath}](img11.gif)
Similarly, the parameters ![]() and
and ![]() for the first and
second layers can be defined as follows:
for the first and
second layers can be defined as follows:
![]()
![\begin{displaymath}
{\bf W}_2 =
\left[
\begin{array}
{cc}
w_{25} & w_{26} \\
...
... \\
w_{45} & w_{46} \\
w_{5} & w_{6} \\ \end{array}\right]\end{displaymath}](img15.gif)
The equations for computing the output of the first layer are
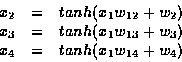
![]()
![\begin{displaymath}
\left[
\begin{array}
{ccc}
x_{2,1} & x_{3,1} & x_{4,1} \\ \v...
... w_{14} \\ w_{2} & w_{3} & w_{4} \\ \end{array}\right]
\right),\end{displaymath}](img18.gif)
![]()
tanmlp.m:
X1 = tanh([X0 one]*W1);
tanmlp.m:
X2 = tanh([X1 one]*W2);
The instantaneous error measure for the pth data pair is defined by
Ep = (t5,p-x5,p)2 + (t6,p-x6,p)2,
where t5,p and t6,p are the pth target outputs; x5,p and x6,p are the pth network outputs. The derivative of the above instantaneous error measure with respect to the network outputs is written as![]()
![\begin{displaymath}
\begin{array}
{rcl}
\frac{\textstyle \partial E}{\textstyle ...
...nd{array} \right]
\right)
=
-2 ({\bf T}- {\bf X}_2),\end{array}\end{displaymath}](img21.gif)
tanmlp.m:
dE_dX2 = -2*(T - X2);
Now we can compute the derivatives of Ep with respect to the second-layer's weights and bias. The derivatives of Ep with respect to the parameters (weights and bias) of node 5 are
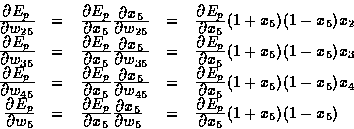
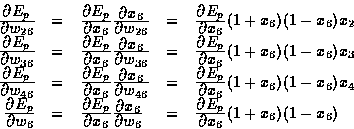
![\begin{displaymath}
\frac{\textstyle \partial E_p}{\textstyle \partial {\bf W}_2...
... E_p}{\textstyle \partial x_6}(1-x_6)(1+x_6)\end{array}\right].\end{displaymath}](img24.gif)
Therefore the accumulated gradient vector is
![\begin{displaymath}
\begin{array}
{rcl}
\frac{\textstyle \partial E}{\textstyle ...
... {\bf X}_2}.*(1+{\bf X}_2).*(1-{\bf X}_2)
\right]\\ \end{array}\end{displaymath}](img25.gif) |
(1) |
tanmlp.m:
dE_dW2 = [X1 one]'*(dE_dX2.*(1+X2).*(1-X2));
For derivatives of Ep with respect to x2, we have
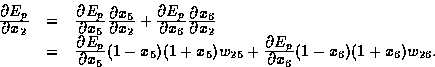
Similarly, we have
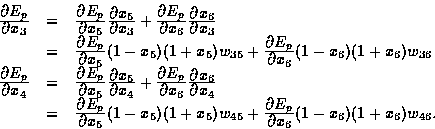
The preceding three equations can be put into matrix form:
![\begin{displaymath}
\begin{array}
{rcl}
\left[
\frac{\textstyle \partial E_p}{\...
...& w_{36}\\ w_{45} & w_{46}\\ \end{array}\right]^T\\ \end{array}\end{displaymath}](img28.gif)
Hence the accumulated derivatives of E with respect to ![]() are
are
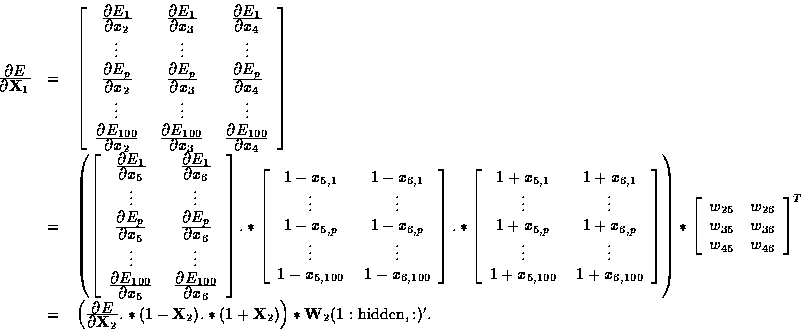
The preceding equation corresponds to line 62 of tanmlp.m:
dE_dX1 = dE_dX2.*(1-X2).*(1+X2)*W2(1:hidden_n,:)';
By proceeding as what we have done in Equation (1), we have
![\begin{displaymath}
\begin{array}
{rcl}
\frac{\textstyle \partial E}{\textstyle ...
... {\bf X}_1}.*(1+{\bf X}_1).*(1-{\bf X}_1)
\right]\\ \end{array}\end{displaymath}](img30.gif)
tanmlp.m:
dE_dW1 = [X0 one]'*(dE_dX1.*(1+X1).*(1-X1));